
Yes, that’s 10,000 cities! Over these last six months, I’ve been busy and am excited to share this.
I first worked with Genetic Algorithms many years back as part of an ESA study into what was then to be a vision system for a future Mars rover. I was only a young lad at the time. Since then, I’ve always been itching to write my own implementation. Over recent months, I’ve been working with crypto-currency trading algorithms for which I need fast search optimization. So this was the perfect opportunity.
A Little Background
Travelling Salesman Problem
The TSP, or “travelling salesman problem”, is an NP-hard computational problem. In short, a salesman needs to visit a number of cities and obviously wants to find the shortest route between them. If the number of cities is small, say 10, we can just look at them a draw a route between each ourselves. However, as the number of cities becomes larger, the number of possible routes explodes according to a polynomial relationship.
Genetic Algorithms
A genetic algorithm is a search optimization technique which derives inspiration from biological notions concerning genetics and evolution. In short, we “breed” candidate solutions to the problem we want to solve and let them evolve. This is an approach used to train neural networks, but we can also apply it to TSP.
Evolgen – My C# Implementation
I’ve worked with C++ throughout much of my career. However, I chose C# and .NETCORE for my wider trading project, hence my genetic algorithm is written in C# also.
In order to render the output, I had to write a demo “test bed”. I’ve been working with C# for a while with console based projects on Linux, but this would be my first WPF desktop application. However, I am familiar with writing desktop applications and, in particular, Qt for C++ and found the development approach of WPF (in terms of form layout and design) remarkably similar. So it was a natural step for me and what you see below took me about a week to write.
I expected initially that EVOLGEN would have no problem solving for a 100 cities, but was a little surprised when it did so more or less instantly. So I started upping the city count (thus making the problem more difficult to solve).
Performance
Here are some screen grabs showing its evolution with 10,000 cities over a 10 hour period. We can see that the first one, just after evolution begins, looks like a solid mess. Looking at this, it is hard to believe that it will untangle this monstrous knot.
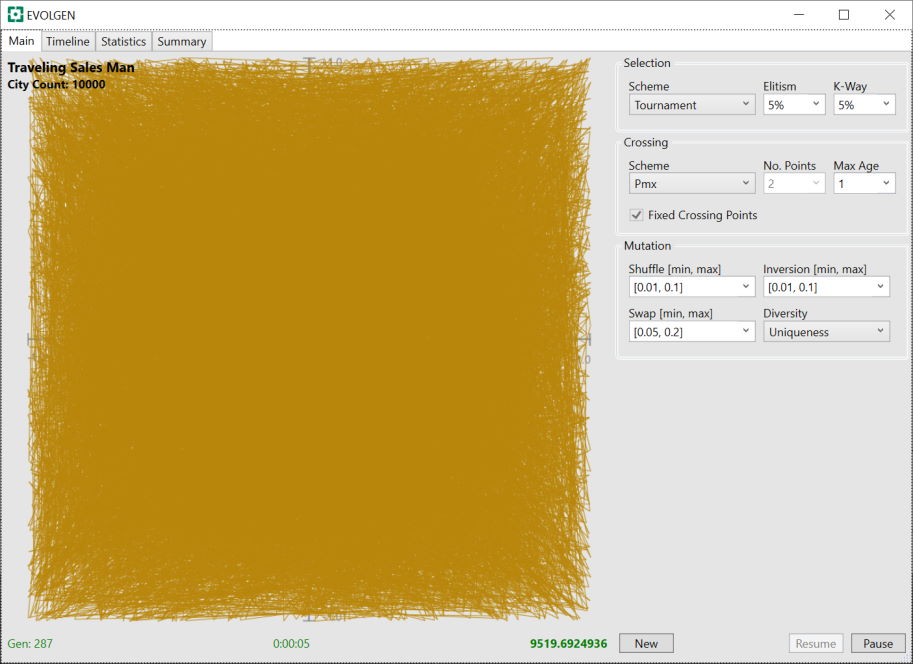
In these views, “cities” are plotted on a grid in the range [-1.0, +1.0], with a starting point at the origin. The generation number is shown in green bottom left in the screenshot, and the total distance of the route shown bottom right.
After only 5 minutes or so, we can start to see some daylight through the trees.
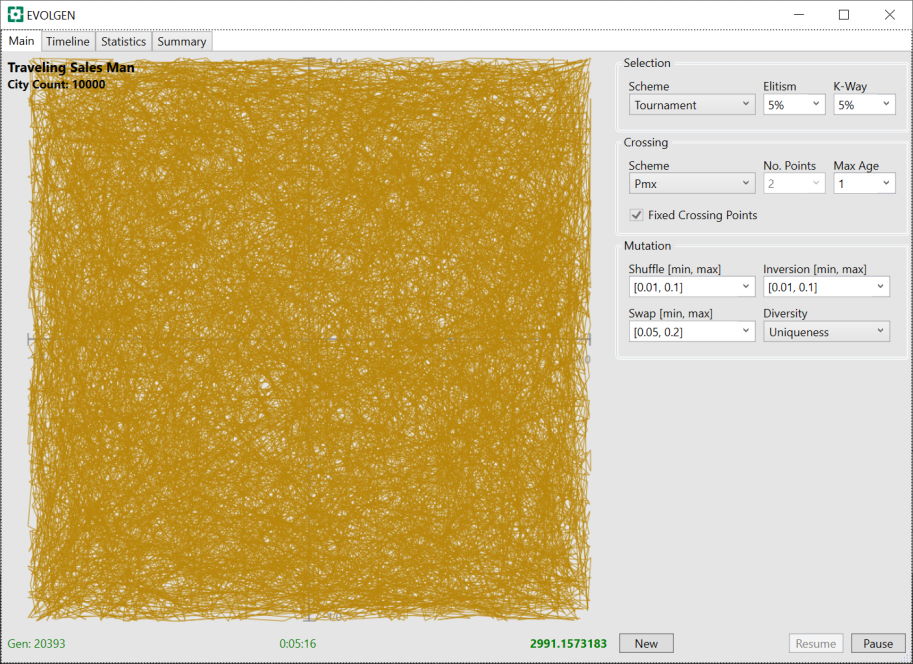
And then the sun shines through:
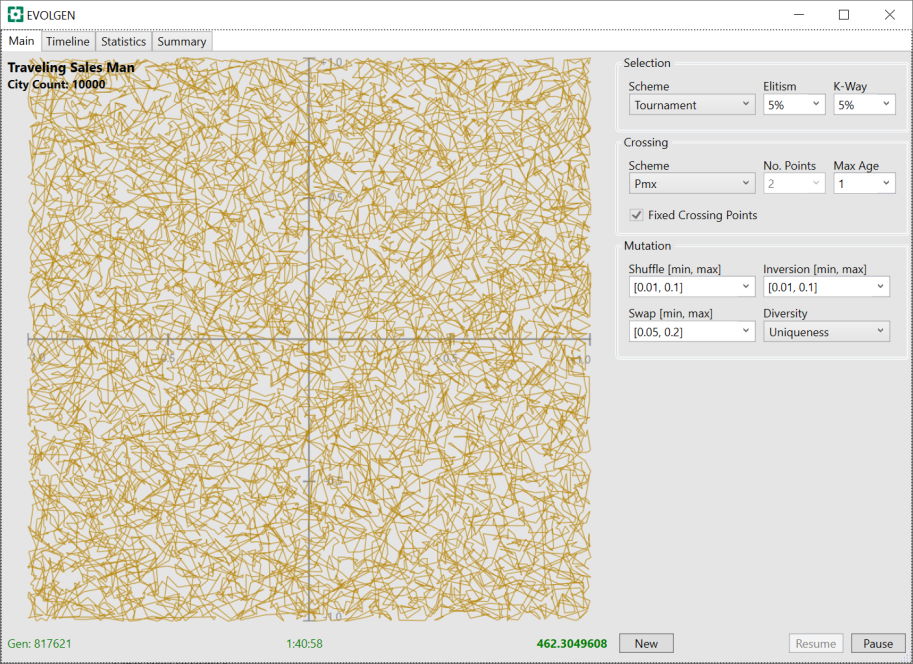
After almost 10 hours (below), I decided my CPU had suffered enough. We can see that the route distance has come down from 9519, early in the evolution, to a mere 218 below.
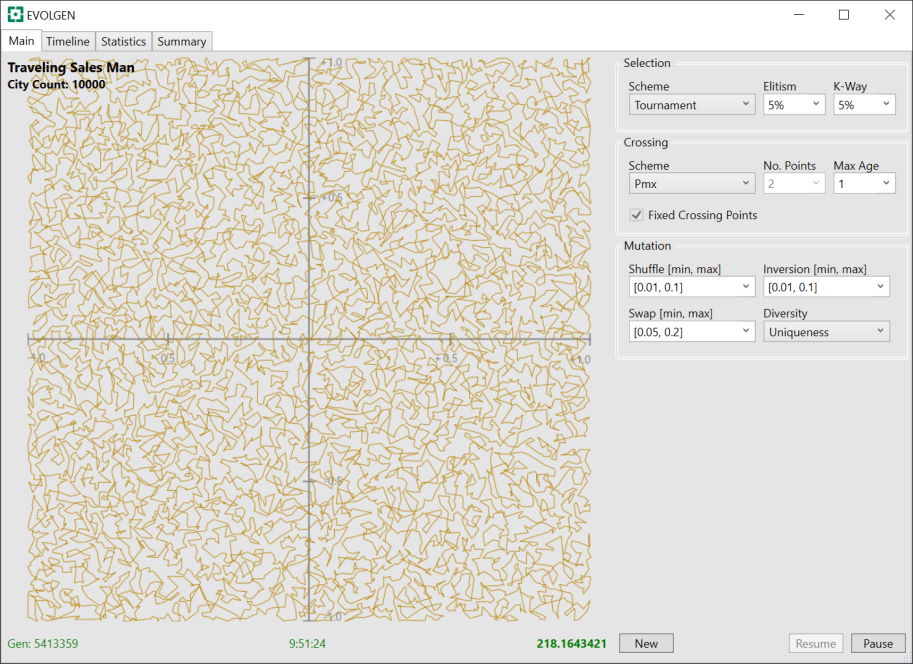
Now, the above is running with a single thread only on an i7-6700. EVOLGEN is designed to take advantage of multiple threads but what I’m finding it that, unless candidate solutions are individually computationally expensive, then the synchronization between threads detracts from the overall performance. However, I believe I can improve things somewhat in the future.
Other Mathematical Problems
TSP is just one class of problem which, in my case, serves only as a development test-bed and a means to compare performance. Here is EVOLGEN with the Rastrigin test function, a mathematical function used for searching optimization testing.

The trick is to find the global minimum without getting stuck in any of the local minima.
Final thoughts
As part of this project, I also wrote my own pseudo random number library. We can select different generators in EVOLGEN, as shown above. Performance of most of these are better than the System Random class in C#, which helps somewhat. There are actually some very good and fast algorithms now and my personal preference at the moment are the XOSHIRO algorithms by David Blackman and Sebastiano Vigna: Xoshiro / Xoroshiro Generators and the PRNG Shootout.
However, my primary reason for doing this was not just for performance (I suspect its impact is relatively minor), but rather that it was just something I wanted to do. I’m not afraid to re-invent “wheels”, especially if I can make them better. I’m also somewhat interested in the philosophical implications of randomness, but perhaps this is a topic for another time.

